常见排序列表

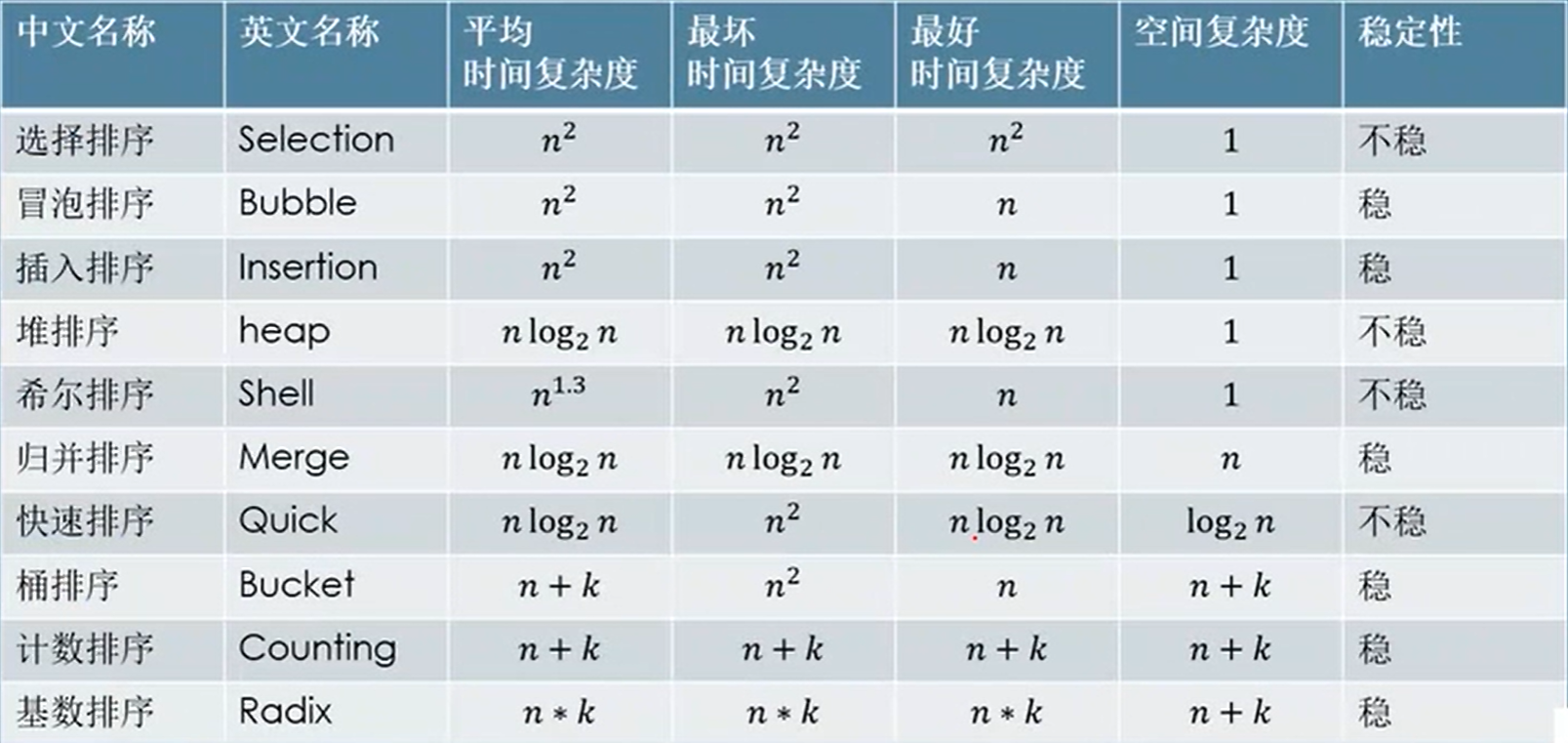
快速记忆上表口诀：

选泡插，
快归堆希统计基，
恩方恩老恩13,
对恩加K恩乘K，
不稳稳稳不稳稳，
不稳不稳稳稳稳！

一下使用的工具方法：

  /**
   * 交换 如果ints [i]> ints [j]，则交换
   *
   * @param ints
   * @param i
   * @param j
   */
  private static void swap(int[] ints, int i, int j) {
    if (ints[i] > ints[j]) {
      int anInt = ints[i];
      ints[i] = ints[j];
      ints[j] = anInt;
    }
  }

选择排序

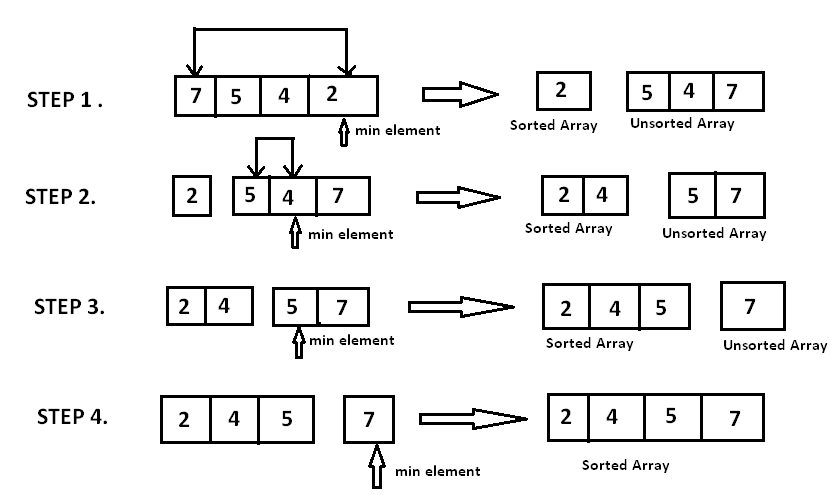
简单选择排序: 简单选择排序的基本思想非常简单，即：第一趟，从 n 个元素中找出关键字最小的元素与第一个元素交换；第二趟，在从第二个元素开始的 n-1 个元素中再选出关键字最小的元素与第二个元素交换；如此，第 k 趟，则从第 k 个元素开始的 n-k+1 个元素中选出关键字最小的元素与第 k 个元素交换，直到整个序列按关键字有序。

  private static int[] sort(int[] ints) {
    for (int i = 0; i < ints.length-1; i++) {
      for (int j = i + 1; j <ints.length ; j++) {
        swap(ints, i, j);
      }
    }
    return ints;
  }

冒泡排序

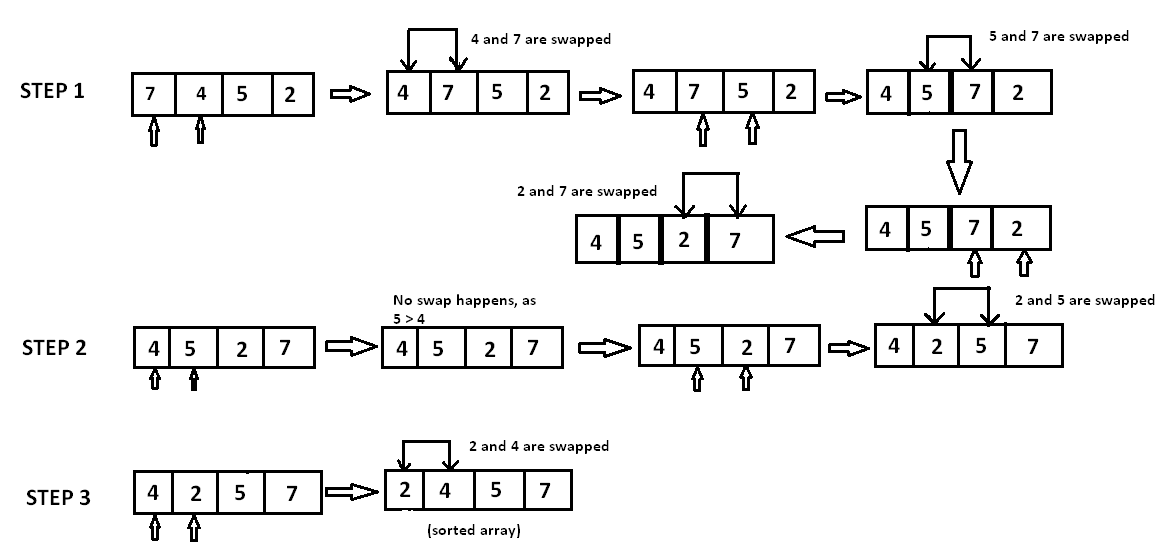
简单冒泡排序：冒泡排序的思想非常简单。首先，将 n 个元素中的第一个和第二个进行比较，如果两个元素的位置为逆序，则交换两个元素的位置；进而比较第二个和第三个元素关键字，如此类推，直到比较第 n-1 个元素和第 n 个元素为止；上述过程描述了冒泡排序的第一趟排序过程，在第一趟排序过程中，我们将关键字最大的元素通过交换操作放到了具有 n 个元素的序列的最一个位置上。然后进行第二趟排序，在第二趟排序过程中对元素序列的前 n-1 个元素进行相同操作，其结果是将关键字次大的元素通过交换放到第 n-1 个位置上。一般来说，第 i 趟排序是对元素序列的前 n-i+1 个元素进行排序，使得前 n-i+1 个元素中关键字最大的元素被放置到第 n-i+1 个位置上。排序共进行 n-1 趟，即可使得元素序列按关键字有序。

private static int[] bubblesort(int[] ints) {
    for (int i = ints.length - 1; i >= 0; i--) {
      for (int j = 0; j < i; j++) {
        swap(ints, j, j + 1);
      }
    }
    return ints;
}

插入排序

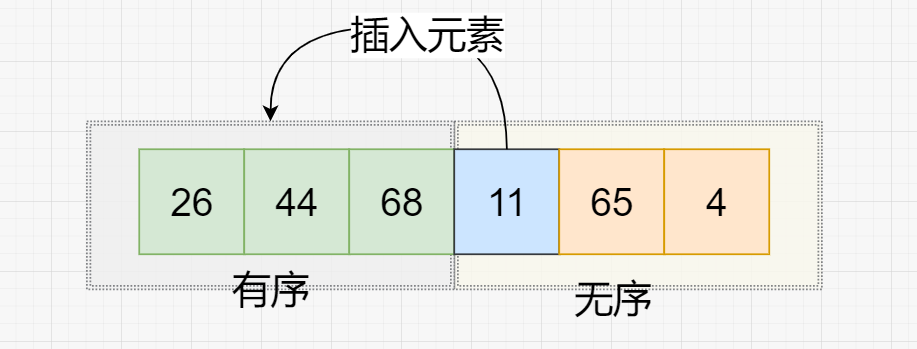
直接插入排序：（类似玩扑克牌，手中已经是有序的，将每次新拿到的牌插入到手中有序的中）
直接插入排序是一种最简单的插入排序方法，它的基本思想是：仅有一个元素的序列总是有序的，因此，对 n 个记录的序列，可从第二个元素开始直到第 n 个元素，逐个向有序序列中执行插入操作，从而得到 n 个元素按关键字有序的序列。一般来说，在含有 j-1 个元素的有序序列中插入一个元素的方法是：从第 j-1 个元素开始依次向前搜索应当插入的位置，并且在搜索插入位置的同时可以后移元素，这样当找到适当的插入位置时即可直接插入元素。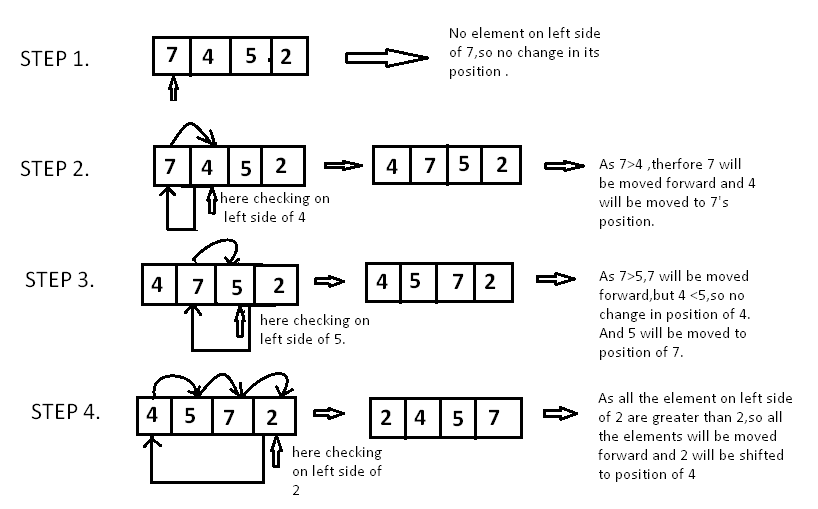

  private static int[] insertSort(int[] ints) {
    for (int i = 1; i < ints.length; i++) {
      for (int j = i; j > 0; j--) {
        swap(ints, j - 1, j);
      }
    }
    return ints;
  }

希尔排序

希尔排序又称为“缩小增量排序”，它也是一种属于插入排序类的排序方法，是一种对直
接插入排序的改进，但在时间效率上却有较大的改进。
从对直接插入排序的分析中知道，虽然直接插入排序的时间复杂度为O(n2)，但是在待排序元素序列有序时，其时间复杂度可提高至O(n)。由此可知在待排序元素基本有序时，直接插入排序的效率可以大大提高。从另一方面看，由于直接插入排序方法简单，则在n值较小时效率也较高。希尔排序正是从这两点出发，对直接插入排序进行改进而得到的一种排序方法。

希尔排序的基本思想是：首先将待排序的元素分为多个子序列，使得每个子序列的元素个数相对较少，对各个子序列分别进行直接插入排序，待整个待排序序列“基本有序”后，再对所有元素进行一次直接插入排序。

根据上述排序思想，下面我们给出希尔排序的排序过程：
⑴ 选择一个步长序列t1， t2， …， tk，其中ti>tj（i<j）， tk=1；
⑵ 按步长序列个数 k，对待排序元素序列进行 k 趟排序；
⑶ 每趟排序，根据对应的步长ti，将待排序列分割成ti个子序列，分别对各子序列进行直接插入排序。
当步长因子为 1 时，所有元素作为一个序列来处理，其长度为 n。

  private static int[] shellSort(int[] ints) {
    for (int gep = ints.length / 2; gep > 0; gep /= 2) {
      for (int i = gep; i < ints.length; i++) {
        for (int j = i; j > gep - 1; j -= gep) {
          swap(ints, j - gep, j);
        }
      }
    }
    return ints;
  }

归并排序 (Java 对象默认排序 TimSort 基数排序的一种)

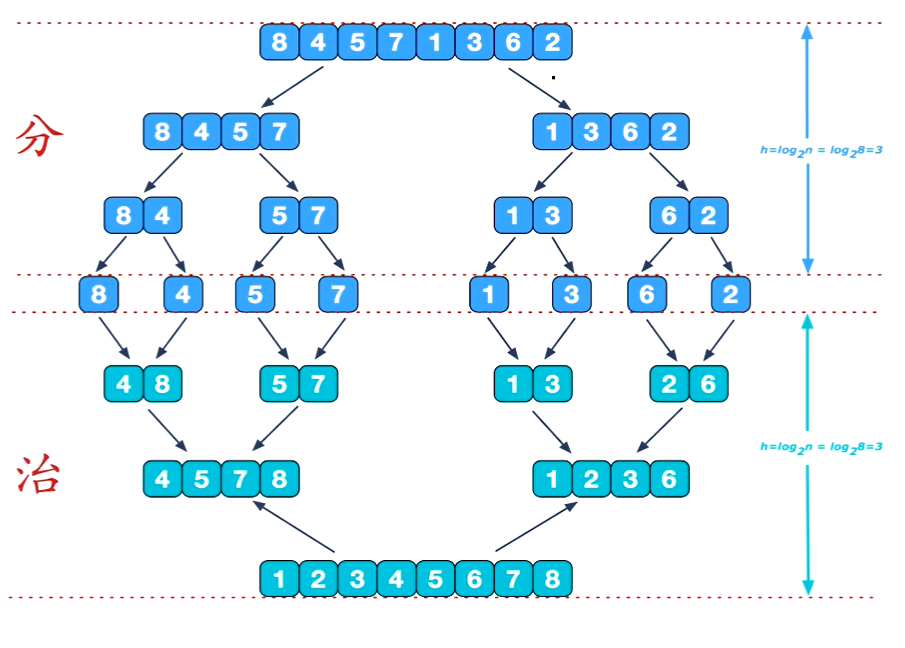
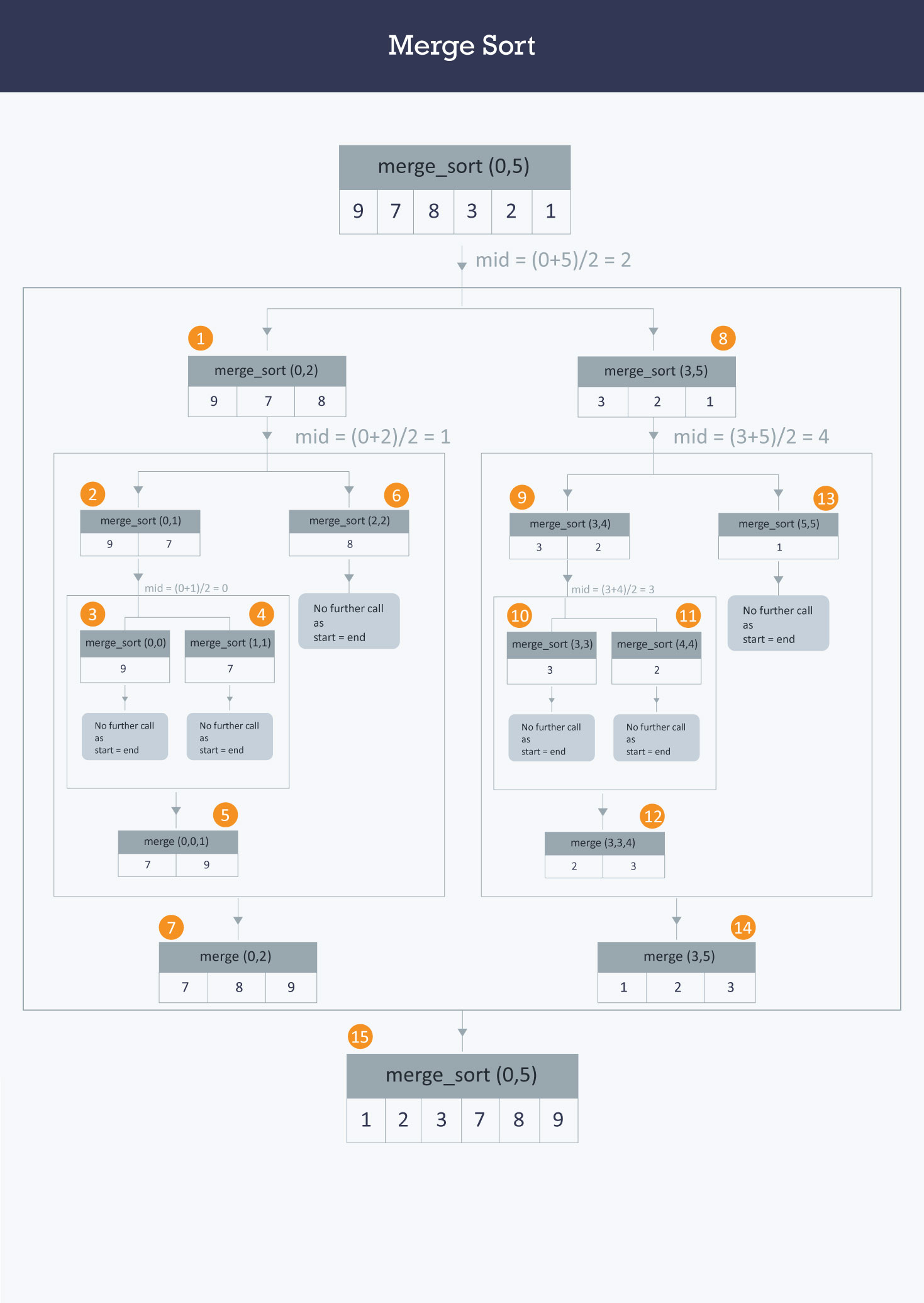
归并排序：

1. 将序列中带排序数字分为若干组，每个数字分为一组
2. 将若干个组两两合并，保证合并后的组是有序的
3. 重复第二步操作直到只剩下一组，排序完成

  private static int[] mergeSort(int[] ints) {
    mergeSort(ints, 0, ints.length - 1);
    return ints;
  }

  private static void mergeSort(int[] a, int low, int hight) {
    // 如果已经分割到单个元素了就直接结束分割
    if (low >= hight) return;

    int mid = (hight + low) >> 1;
    mergeSort(a, low, mid);
    mergeSort(a, mid + 1, hight);
    // 合并
    merge(a, low, mid, hight);
  }

  /**
   * 数据元素数组 a， a 待合并的两个有序区间[p..q]以及[q+1..r]
   * 如 ：   [6, 7, 9, 1, 3, 4]
   * 合并后：[6, 7, 9, 1, 3, 4]
   * @param a 前后有序数组
   * @param low 开始位置
   * @param mid 中间不同序位置
   * @param hight 结束位置
   */
  private static void merge(int[] a, int low, int mid, int hight) {
    int[] ints = new int[hight - low + 1];
    int l = low;
    int h = mid + 1;
    int indexInts = 0;
    while (l <= mid && h <= hight) ints[indexInts++] = a[l] <= a[h] ? a[l++] : a[h++];
    while (l <= mid) ints[indexInts++] = a[l++];
    while (h <= hight) ints[indexInts++] = a[h++];
    System.arraycopy(ints, 0, a, low, ints.length);
  }

快速排序

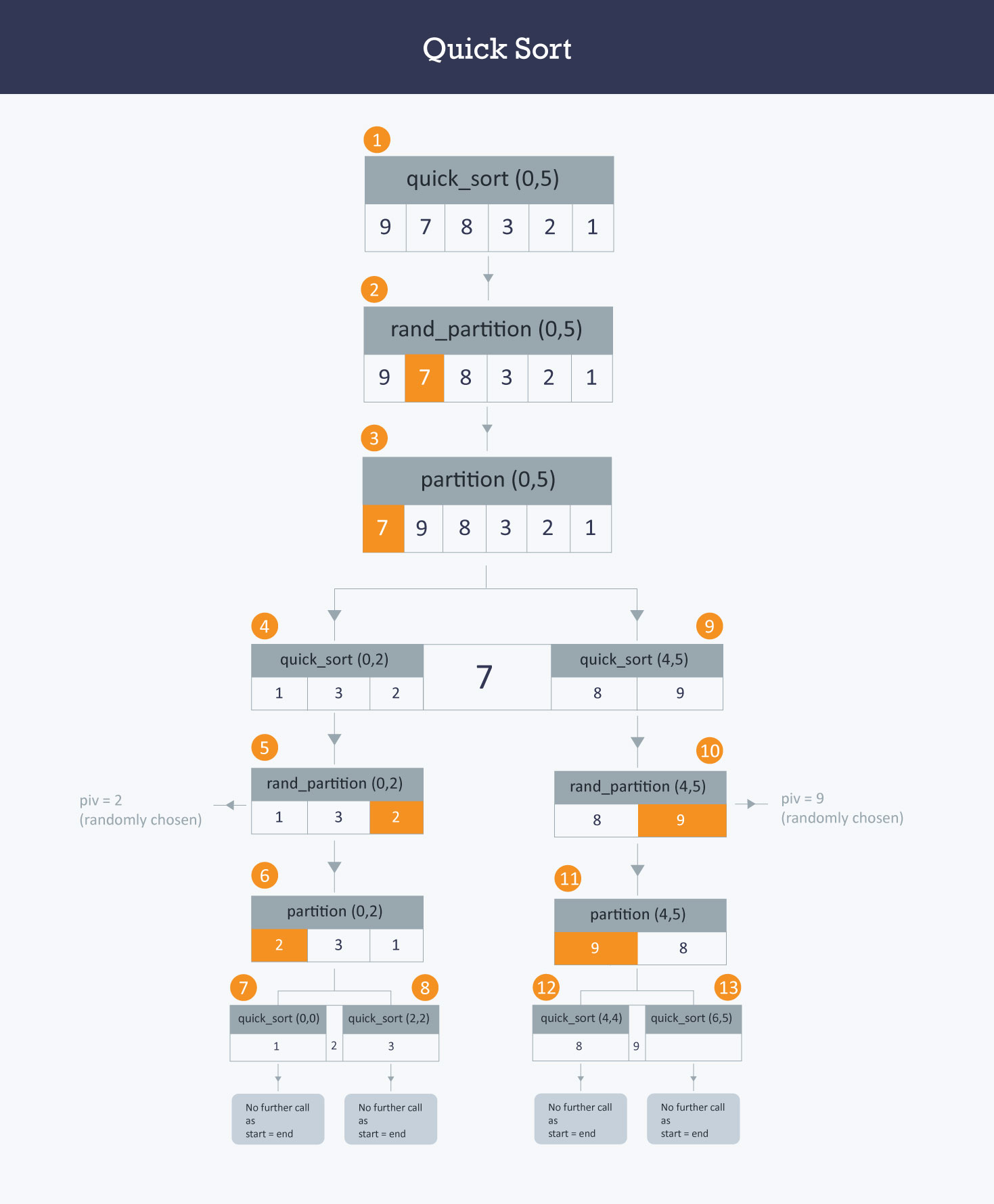
快速排序的原理：选择一个关键值作为基准值。比基准值小的都在左边序列（一般是无序的），比基准值大的都在右边（一般是无序的）。 一般选择序列的第一个元素。
一次循环： 从后往前比较，用基准值和最后一个值比较，如果比基准值小的交换位置，如果没有继续比较下一个，直到找到第一个比基准值小的值才交换。 找到这个值之后，又从前往后开始比较，如果有比基准值大的，交换位置，如果没有继续比较下一个，直到找到第一个比基准值大的值才交换。直到从前往后的比较索引>从后往前比较的索引，结束第一次循环，此时，对于基准值来说，左右两边就是有序的了。

  private static int[] quickSort(int[] ints) {
    quickSort(ints, 0, ints.length - 1);
    return ints;
  }

  private static void quickSort(int[] ints, int low, int high) {
    if (low >= high) return;

    int pivot = partition(ints, low, high);

    quickSort(ints, low, pivot - 1);
    quickSort(ints, pivot + 1, high);
  }

  private static int partition(int[] ints, int low, int high) {
    int l = low;
    int h = high - 1;
    int pivot = ints[high];

    while (l <= h) {
      while (l <= h && ints[l] <= pivot) l++;
      while (l <= h && ints[h] > pivot) h--;
      if (l < h) {
        swap(ints, l, h);
        l++;
        h--;
      }
    }
    swap(ints, l, high);

    return l;
  }

计数排序

计数排序是一种非基于比较的排序算法，其空间复杂度和时间复杂度均为 O(n+k)，其中 k 是整数的范围。基于比较的排序算法时间复杂度最小是 O(nlogn)的。

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

• 花费 O(n)的时间扫描一下整个序列 A，获取最小值 min 和最大值 max
• 开辟一块新的空间创建新的数组 B，长度为 ( max - min + 1)
• 数组 B 中 index 的元素记录的值是 A 中某元素出现的次数
• 最后输出目标整数序列，具体的逻辑是遍历数组 B，输出相应元素以及对应的个数

  /**
   * 计数排序
   * @param ints 待排序数组
   * @param min 范围->数组中最小值
   * @param max 范围->数组中过最大值
   */
  private static void countingSort(int[] ints, int min, int max) {

    int[] count = new int[max - min + 1];
    int[] newInts = new int[ints.length];

    for (int i = 0; i < ints.length; i++) count[ints[i]] += 1;

    for (int i = 0, index = 0; i < count.length; i++) {
      int ct = count[i];
      while (ct-- > 0) newInts[index++] = i;
    }
    System.arraycopy(newInts, 0, ints, 0, ints.length);
  }

基数排序

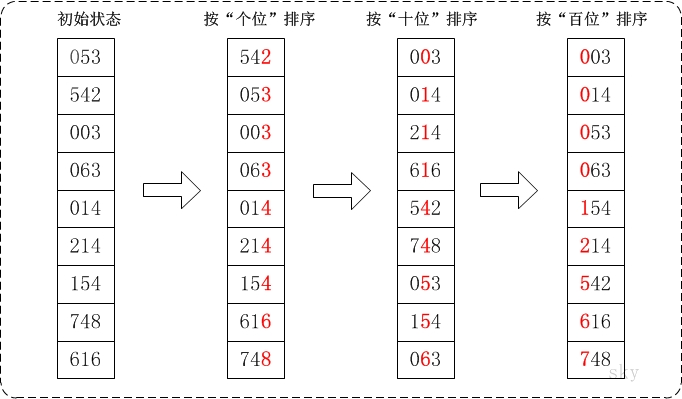
基数排序(Radix Sort)是桶排序的扩展，它的基本思想是：将整数按位数切割成不同的数字，然后按每个位数分别比较。
具体做法是：将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

public void radixSort(int[] array) {

    int max = array[0];
    for (int i = 0; i < array.length; i++) { // 找到数组中的最大值
      if (array[i] > max) {
        max = array[i];
      }
    }

    int keysNum = 0; // 关键字的个数，我们使用个位、十位、百位...当做关键字，所以关键字的个数就是最大值的位数
    while (max > 0) {
      max /= 10;
      keysNum++;
    }
    List<ArrayList<Integer>> buckets = new ArrayList<ArrayList<Integer>>();
    for (int i = 0; i < 10; i++) { // 每位可能的数字为0~9，所以设置10个桶
      buckets.add(new ArrayList<Integer>()); // 桶由ArrayList<Integer>构成
    }

    for (int i = 0; i < keysNum; i++) { // 由最次关键字开始，依次按照关键字进行分配
      for (int j = 0; j < array.length; j++) { // 扫描所有数组元素，将元素分配到对应的桶中
        // 取出该元素对应第i+1位上的数字，比如258，现在要取出十位上的数字，258%100=58,58/10=5
        int key = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
        buckets.get(key).add(array[j]); // 将该元素放入关键字为key的桶中
      }
      // 分配完之后，将桶中的元素依次复制回数组
      int counter = 0; // 元素计数器
      for (int j = 0; j < 10; j++) {
        ArrayList<Integer> bucket = buckets.get(j); // 关键字为j的桶
        while (bucket.size() > 0) {
          array[counter++] = bucket.remove(0); // 将桶中的第一个元素复制到数组，并移除
        }
      }
    }
  }