数据结构
简单整理
数据的基本概念
- 数据
数值和符号集合
数据项
具有原子性,最小数据单位
数据元素
数据基本单位,是数据集合的个体,通常由若干个数据项组成
数据对象
性质相同的数据元素的集合,是数据的一部分
逻辑结构
线性结构
- 栈、对,串,线性表、数组
非线性结构
树结构
图结构
树
二叉树
二叉树的实现
遍历 :Traverse
- 先序
- 中序
- 后序
- 层次遍历:队列/栈:(将root先入队,后出队,将root的左节点和右键点放入队列。。。依次循环)
图
定义
存储
- 邻接矩阵:二维数组 顺序存储结构
- 邻接表:链表 链式存储结构
遍历
深度优先遍历:类似树的先根遍历(递归,非递归)
广度优先遍历:类似树的层次遍历(非递归)
最短路径
- 1、段数最少:广度优先搜索
- 2、权值和最小:迪克特斯拉算法
存储结构
- 顺序存储
- 链式存储
- 索引存储
- 散列存储
数据运算
- 索引、排序,插入、删除、修改。。。
详细了解
1. 队列
概念:
队列是一个有序列表,可以用数组或是链表来实现。
遵循先入先出的原则。即:先存入队列的数据,要先取出。后存入的要后取出
数组模拟队列
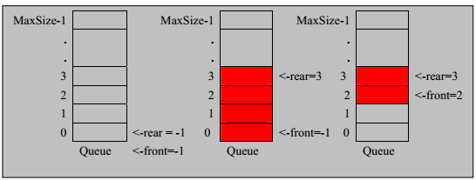
队列本身是有序列表,若使用数组的结构来存储队列的数据,则队列数组的声明如下图, 其中 maxSize 是该队列的最大容量。
因为队列的输出、输入是分别从前后端来处理,因此需要两个变量 front*及 *rear 分别记录队列前后端的下标,front 会随着数据输出而改变,而 rear 则是随着数据输入而改变,如图所示:
思路分析
- 将尾指针往后移:rear+1 , 当front == rear 【空】
- 若尾指针 rear 小于队列的最大下标 maxSize-1,则将数据存入 rear所指的数组元素中,否则无法存入数据。 rear == maxSize - 1[队列满]
循环队列
对前面的数组模拟队列的优化,充分利用数组. 因此将数组看做是一个环形的。(通过取模的方式来实现即可)
分析说明
尾索引的下一个为头索引时表示队列满,即将队 列容量空出一个作为约定,这个在做判断队列满的 时候需要注意 (rear + 1) % maxSize == front 满]
rear == front [空]
class CircleQueue {
private int maxSize;
private int[] arr; // 该数组存放数据,模拟队列
private int front; // 指向队列头部
private int rear; // 指向队列的尾部
public CircleQueue(int arrMaxSize) {
maxSize = arrMaxSize;
arr = new int[maxSize];
}
public boolean isFull() {
//尾索引的下一个为头索引时表示队列满,即将队列容量空出一个作为约定(!!!)
return (rear + 1) % maxSize == front;
}
public boolean isEmpty() {
return this.rear == this.front;
}
public void addQueue(int n) {
if (isFull()) {
System.out.println("队列满,无法加入..");
return;
}
arr[rear] = n;
rear = (rear + 1) % maxSize;
}
public int getQueue() {
if (isEmpty()) {
throw new RuntimeException("队列空~");
}
int value = arr[front];
front = (front + 1) % maxSize;
return value;
}
}
/*
rear 是队列最后元素[含]
front 是队列最前元素[不含]
出队列操作getQueue
显示队列的情况showQueue
查看队列头元素headQueue
退出系统exit
*/2、链表(Linked List)
简介
链表是有序的列表
链表随机位置插入、删除数据时比线性表快,遍历比线性表慢。
链表是以节点的方式来存储,是链式存储
每个节点包含 data 域, next 域:指向下一个节点.
各个节点不一定是连续存储
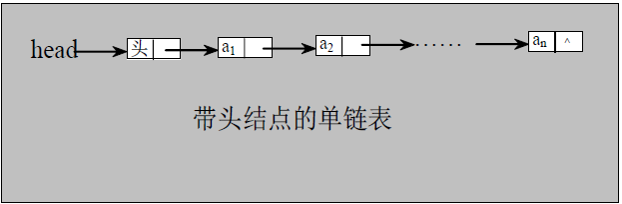
链表分带头节点的链表和没有头节点的链表,根据实际的需求来确定
链表的简单操作
添加:
public void add(Node node){
Node head = this.hear;
while(head.next){
head = head.next;
}
head.next = node;
}
部分源码:
public class LinkedList<e>
extends AbstractSequentialList<e>
implements List<e>, Deque<e>, Cloneable, java.io.Serializable
{
//头尾节点
transient Node<e> first;
transient Node<e> last;
}
//节点类
private static class Node<e> {
//节点存储的数据
E item;
Node<e> next;
Node<e> prev;
Node(Node<e> prev, E element, Node<e> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}由此也可以看出,源码中的链表为双向链表
3、栈
栈简介
栈是一个先入后出(FILO-First In Last Out)的有序列表
栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端,为变化的一端,称为栈顶(Top),另一端为固定的一端,称为栈底(Bottom)
根据栈的定义可知,最先放入栈中元素在栈底,最后放入的元素在栈顶,而删除元素刚好相反,最后放入的元素最先删除,最先放入的元素最后删除
出栈(pop)和入栈(push)的概念(如图所示)
入栈: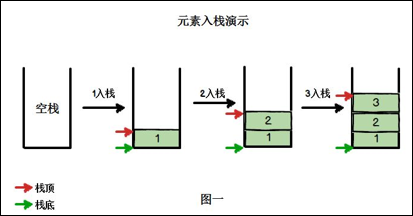
出栈: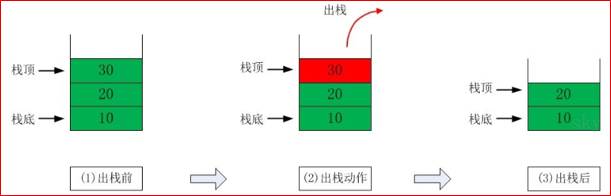
应用场景
子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中。
处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。
二叉树的遍历。
图形的深度优先(depth一first)搜索法。
Java栈的通用接口
package com.stack;
public interface Stack {
public int getSize();//返回栈中元素个数
public boolean isEmpty();//判断栈是否为空
public Object top();//获取栈顶元素,但不删除
public void push(Object elem);//入栈
public Object pop();//出栈
}
基于数组实现:
package com.stack;
public class MyStack implements Stack{
public static final int CAPACITRY = 1024;
public int capacity;
public Object[] s;
public int top = -1;
public MyStack()
{
this(CAPACITRY);
}
public MyStack(int cap) {
capacity = cap;
s = new Object[capacity];
}
@Override
public int getSize() {
return top+1;
}
@Override
public boolean isEmpty() {
return (top < 0);
}
@Override
public Object top() {
if(isEmpty())
{
System.out.println("栈为空");
return null;
}
return s[top];
}
@Override
public void push(Object elem) {
if(getSize() == capacity)
{
System.out.println("栈满");
return;
}
s[++top] = elem;
}
@Override
public Object pop() {
if(isEmpty())
{
System.out.println("栈为空");
return null;
}
Object elem = s[top];
s[top--] = null;
return elem;
}
}基于单链表实现栈
节点的java实现
package com.node;
public class Node {
private Object elem;
private Node next;
// 。。。get set construe 。。。
}
栈的实现
package com.stack;
import com.node.Node;
//单链表实现栈
public class Stack_list implements Stack{
protected Node top;//栈顶元素
protected int size;//栈中元素个数
//初始化时创建头结点
public Stack_list()
{
top = null;
size = 0;
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return (top == null)?true:false;
}
@Override
public Object top() {
if(isEmpty())
{
System.out.println("栈为空");
}
return top.getElem();
}
@Override
public void push(Object elem) {
//元素压栈
Node newNode = new Node(elem,top);
top = newNode;//修改栈顶指针
size++;//修改栈中元素个数
}
@Override
public Object pop() {
if(isEmpty())
{
System.out.println("栈为空");
return null;
}
Object elem = top.getElem();
top = top.getNext();
size--;
return elem;
}
}4、哈希表(散列)
简介
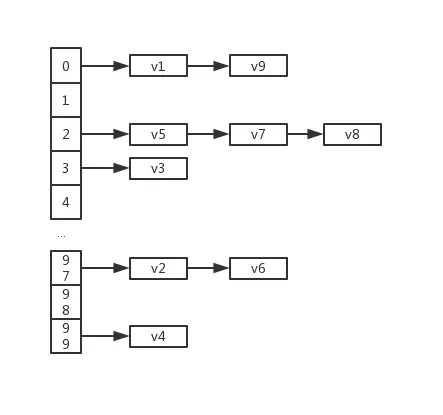
哈希表是由一块地址连续的数组空间构成的,其中每个数组都是一个链表,数组的作用在于快速寻址查找,链表的作用在于快速插入和删除元素,因此,哈希表可以被认为就是链表的数组
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
散列函数
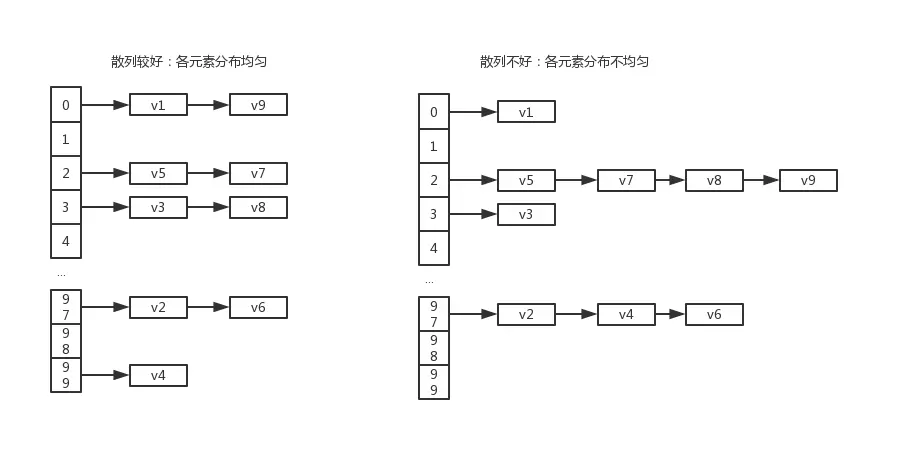
一般而言,我们在存储元素的时候,会用到 “散列函数(散列方法)” ,它的作用就是尽量均衡地将元素分配到数组空间中,避免出现某个数组空间中的链表元素大大超过其它数组空间中链表元素个数的情况
经典的散列函数有“直接定址法”、“数字分析法”、“平方取中法”,“取余法”,“随机数法”
散列冲突
解决方案:
- 开放地址法
- 链地址法 (重)